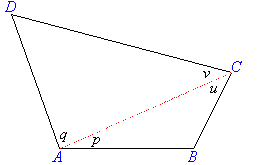
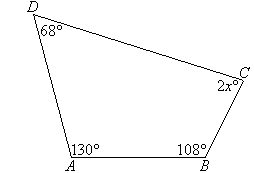
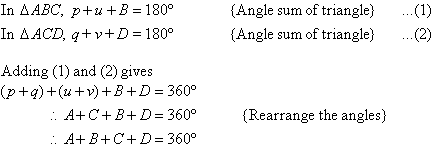Miyerkules, Oktubre 9, 2013

Triangle Congruence Theorems

Triangle Congruence Theorems

On this page, we hope to clear up problems that you might have with proving triangles congruent. Triangles are one of the most used figures in geometry and beyond (engineering), so they are rather important to understand. Scroll down or click any of the links below to start understanding congruent triangles better!

Side-Angle-Side
Side-Side-Side
Angle-Side-Angle
Angle-Angle-Side
CPCTC (Corresponding Parts of Congruent Triangles are Congruent)
Quiz on Congruent Triangles

Side-Angle-Side is a rule used in geometry to prove triangles congruent. The rule states that if two sides and the included angle are congruent to two sides and the included angle of a second triangle, the two triangles are congruent. An included angle is an angle created by two sides of a triangle.

1. Problem: Is triangle PQR congruent to
            triangle STV by SAS? Explain.

  
  Solution: Segment PQ is congruent
              to segment ST because
              PQ = ST = 4.
            Angle Q is congruent to
              angle T because
              angle Q = angle T = 100 degrees.

 Solution: Segment QN is congruent to
              segment QP and segment YN is
              congruent to segment YP because that
              information is given in the figure.
            Segment YQ is congruent to segment
              YQ by the Reflexive Property of Con-
              gruence, which says any figure is 
              congruent to itself.
            Triangle QYN is congruent to triangle
              QYP by Side-Side-Side.

Back to Top

Angle-Side-Angle is a rule used in geometry to prove triangles are congruent. The rule states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, the triangles are congruent. An included side is a side that is common to (between) two angles. For example, in the figure used in the problem below, segment AB is an included side to angles A and B.

1. Problem: Show that triangle BAP is congruent to triangle CDP.

Solution: Angle A is congruent to angle D because they are both right angles. Segment AP is congruent to segment DP be- cause both have measures of 5. Angle BPA and angle CPD are congruent be-

cause vertical angles are congruent.
               Triangle BAP is congruent to triangle CDP
                  by Angle-Side-Angle.

Back to Top

Angle-Angle-Side is a rule used in geometry to prove triangles are congruent. The rule states that if two angles and a nonincluded side of one triangle are congruent to two angles and the corresponding nonincluded side of another triangle, the two triangles are congruent.

1.   Problem: Show that triangle CAB is congruent
              to triangle ZXY.







     Solution: Angle A and angle Y are congruent
                  because that information is given 
                  in the figure.
               Angle C is congruent to angle Z 
                  because that information is given 
                  in the figure.
               Segment AB corresponds to segment XY and
                  they are congruent because that
                  information is given in the figure.
               Triangle CAB is congruent to triangle ZXY
                  by Angle-Angle-Side.

Back to Top

When two triangles are congruent, all six pairs of corresponding parts (angles and sides) are congruent. This statement is usually simplified as corresponding parts of congruent triangles are congruent, or CPCTC for short.

1.   Problem: Prove segment BC is congruent to
              segment CE.
                
  


  
  


     Solution: First, you have to prove that triangle
               CAB is congruent to triangle CED.
               
               Angle A is congruent to angle D 
                  because that information is given 
                  in the figure.
               Segment AC is congruent to segment CD
                  because that information is given
                  in the figure.
               Angle BCA is congruent to angle DCE
                  because vertical angles are
                  congruent.
               Triangle CAB is congruent to triangle CED
                  by Angle-Side-Angle.
               
               
               Now that you know the triangles are 
               congruent, you know that all 
               corresponding parts must be congruent.  
               By CPCTC, segment BC

is congruent to segment CE

Parallel Lines, and Pairs of Angles

Parallel Lines

Lines are parallel if they are always the same distance apart (called "equidistant"), and will never meet. Just remember:

Always the same distance apart and never touching.

The red line is parallel to the blue line in both these cases:


Example 1		Example 2

Parallel lines also point in the same direction.

Pairs of Angles

When parallel lines get crossed by another line (which is called aTransversal), you can see that many angles are the same, as in this example:
These angles can be made into pairs of angles which have special names.

Testing for Parallel Lines

Some of those special pairs of angles can be used to test if lines really are parallel:

If Any Pair Of ...	Example:

Corresponding Angles are equal, or	a = e
Alternate Interior Angles are equal, or	c = f
Alternate Exterior Angles are equal, or	b = g
Consecutive Interior Angles add up to 180°	d + f = 180°

... then the lines are Parallel

Examples

These lines are parallel, because a pair of Corresponding Angles are equal.
	These lines are not parallel, because a pair of Consecutive Interior Angles do not add up to 180° (81° + 101° =182°)
These lines are parallel, because a pair of Alternate Interior Angles are equal

Martes, Oktubre 8, 2013

Quadrilaterals

A quadrilateral is a closed plane figure bounded by four line segments. For example, the figure ABCD shown here is a quadrilateral.

Quadrilateral ABCD has two diagonals in AC and BD.

A line segment drawn from one vertex of a quadrilateral to the opposite vertex is called a diagonal of the quadrilateral. For example, AC is a diagonal of quadrilateral ABCD, and so is BD.

Naming Quadrilaterals

quadrilateral ABDC-wrong

quadrilateral ABCD-correct

In naming quadrilaterals, its vertices shoul be in consecutive order

Main Parts:

(based from the figure above)

Vertices:

Points: A, B, C, D

Segments:

segment AB

segment BC

segment CD

segment DA

Angles:(can be named by single letter)

angle A / DAB

angle B / ABC

angle C / BCD

angle D / CDA

Types of Quadrilaterals

There are special types of quadrilateral:

Properties of Quadrilateral

Four sides (edges)
Four vertices (corners)
The interior angles add up to 360 degrees:

The Rectangle


		means "right angle"
	and	show equal sides

A rectangle is a four-sided shape where every angle is a right angle (90°).

Also opposite sides are parallel and of equal length.

The Rhombus

A rhombus is a four-sided shape where all sides have equal length.

Also opposite sides are parallel and opposite angles are equal.

Another interesting thing is that the diagonals (dashed lines in second figure) meet in the middle at a right angle. In other words they "bisect" (cut in half) each other at right angles.

The Square


		means "right angle"
		show equal sides

A square has equal sides and every angle is a right angle (90°)

Also opposite sides are parallel.

A square also fits the definition of a rectangle (all angles are 90°), and a rhombus (all sides are equal length).

The Parallelogram

A parallelogram has opposite sides parallel and equal in length. Also opposite angles are equal (angles "a" are the same, and angles "b" are the same).

NOTE: Squares, Rectangles and Rhombuses are all Parallelograms!

Example:

A parallelogram with:

all sides equal and
angles "a" and "b" as right angles

is a square!

The Trapezoid (UK: Trapezium)


Trapezoid	Isosceles Trapezoid

A trapezoid (called a trapezium in the UK) has a pair of opposite sides parallel.

It is called an Isosceles trapezoid if the sides that aren't parallel are equal in length and both angles coming from a parallel side are equal, as shown.

And a trapezium (UK: trapezoid) is a quadrilateral with NO parallel sides:

	Trapezoid	Trapezium
US:	a pair of parallel sides	NO parallel sides
UK:	NO parallel sides	a pair of parallel sides

The Kite

Hey, it looks like a kite. It has two pairs of sides. Each pair is made up of adjacent sides that are equal in length. The angles are equal where the pairs meet. Diagonals (dashed lines) meet at a right angle, and one of the diagonal bisects (cuts equally in half) the other.Sum of the Interior Angles

Sum of the Interior Angles